Você já sonhou em ter uma cozinha ou banheiro único e exclusivo? Agora é possível, graças a matemáticos da Universidade de Arkansas, que descobriram a primeira forma capaz de cobrir uma parede sem repetir o padrão.
Até agora, a chamada “tiling aperiódica” só era possível usando mais de uma forma. Mas este novo modelo, apelidado de “chapéu”, permite que padrões estendidos e infinitos sejam criados apenas com este item.
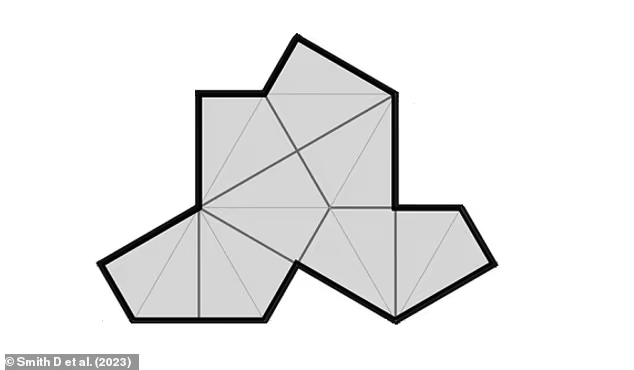
E o mais incrível: essa propriedade aperiódica permanece mesmo quando o tamanho dos 13 lados da forma são mudados, o que significa que existe uma infinidade de possibilidades de padrões.
Os padrões repetidos são comuns em estruturas moleculares de materiais cristalinos, tornando-os mais fáceis de quebrar.
O “chapéu” tem potencial para ser usado na criação de novos materiais mais resistentes e possuir outras propriedades úteis. Até mesmo “novos revestimentos de banheiro” ou “azulejos sofisticados” aparecem como possibilidades nesta recente descoberta matemática.
Desde 1963, com a descoberta de um primeiro jogo de formas aperiódicas, o mundo tem buscado novas maneiras de solucionar este problema matemático.
Os mais famosos são os azulejos de ‘Penrose’, conhecidos por utilizarem dois tipos diferentes de formas para criar os padrões. Mas agora, com a forma de “chapéu”, o céu é o limite.




